こんにちは！ 株式会社GIGの山下です。

今回は、「Tech Trend Talk vol.9 データ処理と機械学習アルゴリズム」のイベントレポートをお届けします。

データ処理と機械学習アルゴリズム

今回の講師は、GIGの技術顧問兼外部取締役の中島正成さん。「データ処理と機械学習アルゴリズム」と題して、機械学習を今後活用してみたいと考えているエンジニア向けに講義を行っていただきました。

中島 正成：株式会社メタップスの取締役CTOとして立ち上げに参画。機械学習とデータサイエンスのプロダクトインプリメントに取り組む。その後、エン・ジャパン株式会社経営戦略室経てIGS株式会社に執行役員CTOとしてジョイン。教育領域へのA.I活用プロダクト開発に取り組む。 

線形回帰のアルゴリズム

回帰とは、説明変数（例：試験勉強に費やした時間）と目的変数（例：試験の結果）の間の関係を表す式を統計的手法によって推計するものです。その中でも「線形回帰」は、データが直線に収束していくような関数を導き出していくことをいいます。 

最小二乗法による最尤（ゆう）推定

週の勉強時間と試験の点数の関係を例に考えてみましょう。Y=点数、X=勉強時間と仮定し、データの収束する関数を Y=aX+b とします。

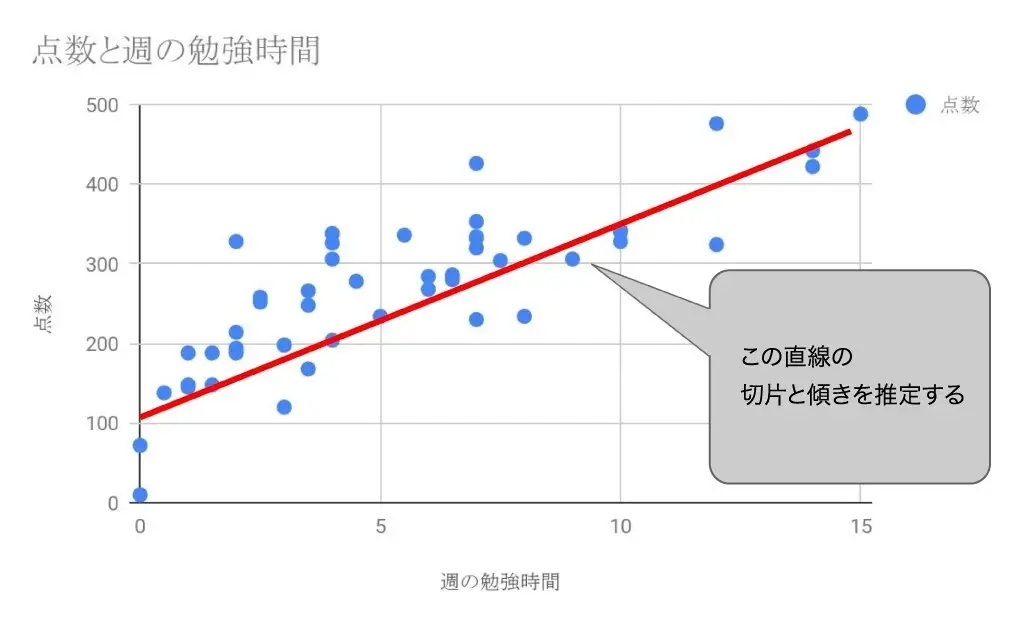
中島さん：「aは傾き、bは切片。傾きと切片の値は、最小二乗法による最尤推定を使って求めていきます」

最小二乗法とは、すべての点と線の距離の誤差を二乗した和がもっとも小さくなるような係数を求める方法です。

最尤推定の「尤」は「もっとも」という意味。すなわち、ざっくりいえば「もっとももっともらしい値を推定する」ということだそうです。「もっとももっともらしい値」とは、確率的にもっとも出現頻度が高くなると予想される値のことです（門外漢の私には少々むずかしい……）。

なぜ点と線の距離の誤差を二乗する必要があるのか、図で考えてみましょう。

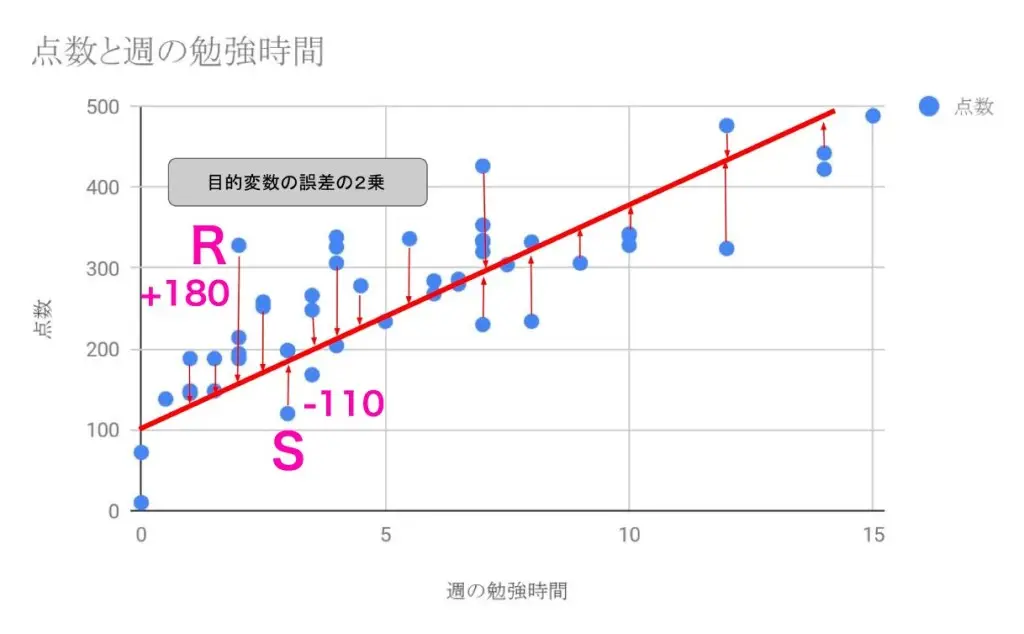
この関数の場合、2時間勉強した人はおよそ150点です。一方、点Rの人は、2時間勉強して330点取っています。つまり点Rから線（関数）までは、330-150=180の誤差があることになります。

また3時間勉強した人は関数上は190点くらいです。しかし、点Sの人は、110点くらいしか取れていません。このときの誤差は、110-190=-80。マイナスの値になります。

プラスとマイナスの値が存在すると、和を計算したときに打ち消しあってしまいます。そのため、誤差を二乗することで、プラスとマイナスを考えないでよくなるのです。

Pythonを使って求める

中島さん：「Pythonの機械学習ライブラリ『scikit-learn』の中の『LinearRegression』を使えば、傾きと切片を求めることができます」

中島さん：「fitで学習させたあとに、coefとinterceptを表示するコードです。coefからは傾き、interceptからは切片が分かります」 

関連記事：中学生レベルの数学で学ぶ、機械学習モデル。まずはPythonライブラリ導入から始めよう！

教師あり学習のパターン認識「サポートベクターマシン」

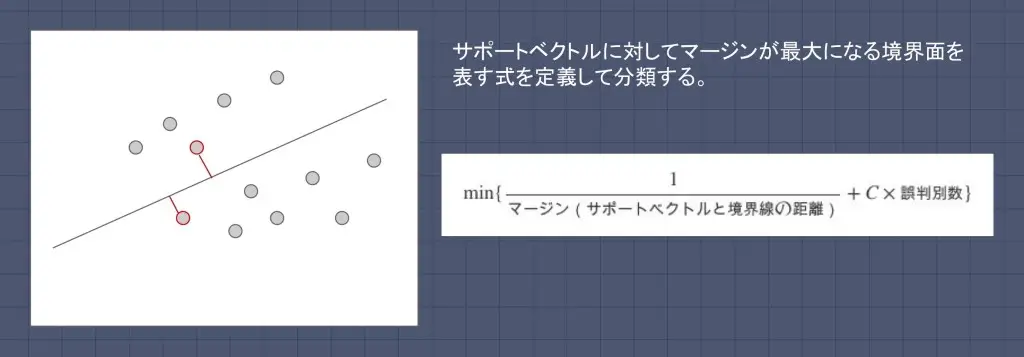
サポートベクターマシン（SVM）は、教師あり学習を用いるパターン認識モデルの一つです。サポートベクトルに対してマージンが最大になる境界面を表す式を定義して、分類を行います。

もう少し噛み砕くて解説します。

複数のグループがあったとき、各グループの端にあるデータ点との距離が最大となるような境界面を求めていきます。各グループの端にあるデータ点のことを「サポートベクトル」と言います。 

SVMの特徴

• 汎用性が高い：多次元のベクトルを超境界面によって分類していくため、正解データを保有するあらゆる分類や回帰に対応できる
• 学習も速くて、予測も早い：カーネル法の恩恵で計算量が少ない
• 尺度の変化に弱い：境界面を引く時にスケーリングを揃えた場合とそうでない場合に分類結果が異なる可能性が高い。事前のデータクリーニング必須。

中島さん：「100点満点のものと、10万点満点のものを同じグラフの中で扱うとした場合、縦と横の尺度を変えてしまうだけで、引く線の場所と角度が異なってきます。汎用性が高い反面、ちょっと手間がかかります。データに応じて適切な尺度を見つけ出すのがSVMの難しさです」 

関連記事：SVM（サポートベクターマシン）を用いた「教師あり学習」をやってみる

複数案のなかから精度を高めるアルゴリズム「ランダムフォレスト」

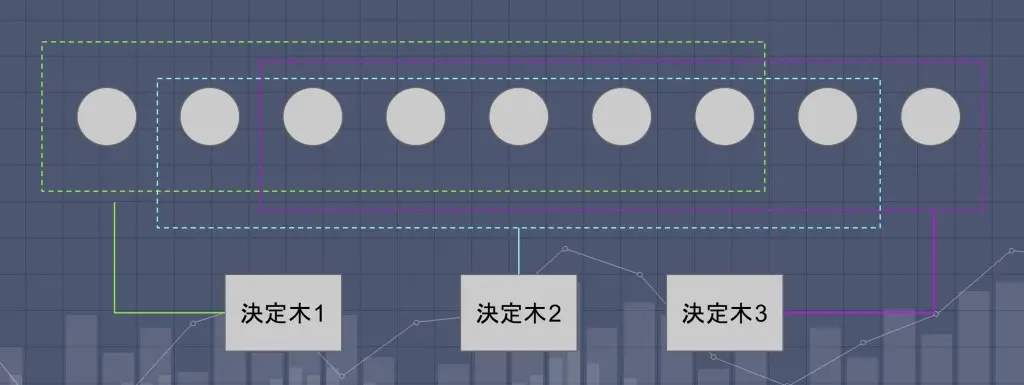
ランダムフォレストとは、ツリー構造の弱分類器（決定木）をたくさんつくって多数決と組み合わせて予測しようというアルゴリズムです。

中島さん：「データの全てを使ってひとつの決定木をつくるのではなく、ランダムに抽出したデータから複数の決定木を生成していきます。データを適切な量に分割して、決定木をたくさん生成することで、多数決による精度を上げていこうとするのが、ランダムフォレストのやりかたです。過学習の影響も小さく、データ量がさほど多くなくてもある程度ワークします」

Pythonのサンプルコード

Pythonの機械学習ライブラリ「scikit-learn」の中に、ランダムフォレストの分類である「RandomForestClassifier」と、ランダムフォレストの回帰である「RandomForestRegressor」が含まれます。

中島さん：「インスタンスを作ったら、トレーニングデータの説明変数の配列と答えの配列を渡して、fitというメソッドで学習します。学習をしたら新しいデータを与えてpredictで予測します。これが基本的な流れです」

関連記事：ランダムフォレストを用いたスコア予測の実践

講義まとめ

まとめ① 非分散・分散データでの使い分け

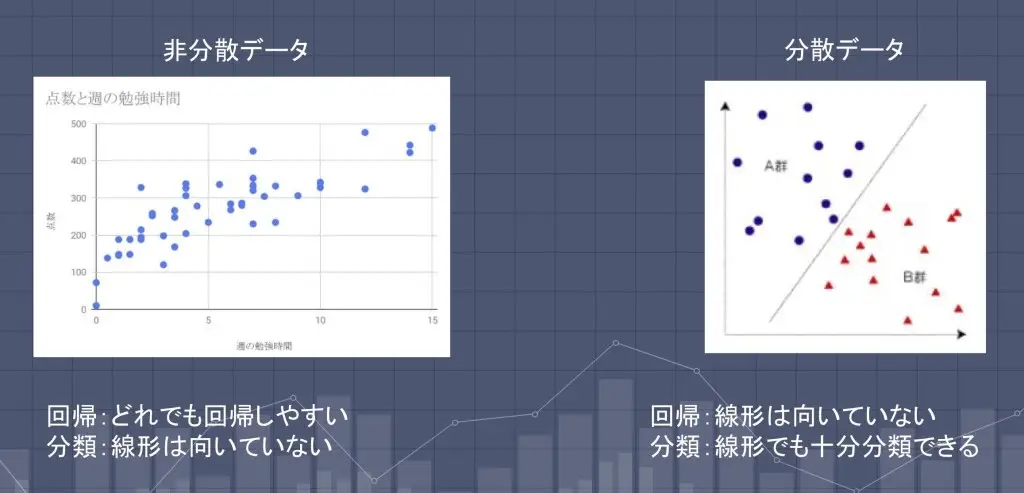
データは、収束している「非分散データ」と、発散している「分散データ」の二つに大きく分けることができます。各データに対して、どの機械学習アルゴリズムが適しているかまとめます。

「非分散データ」に適しているアルゴリズム

• 回帰：線形回帰
• 分類：決定木 / ランダムフォレスト

「分散データ」に適しているアルゴリズム

• 回帰：決定木 / ランダムフォレスト
• 分類：SVMなどの線形分類

中島さん：「機械学習アルゴリズムをWebアプリケーションで使う程度であれば、このときはランダムフォレストだな、線形回帰だなと知っておけば、使い分けることがしやすくなると思います」

まとめ② 回帰アルゴリズムの特徴

線形回帰

• データの相関が明白な場合に精度が上がりやすい
• 分散型データ、外れ値に弱い（異常値はあらかじめ除いておく）

SVM回帰

• 単純な線形回帰よりは分散型データや異常値に強い
• 広くカバーするが、精度を上げにくい

決定木 / ランダムフォレスト回帰

• 割と万能に使える
• 教師データの粒度が荒ければ、答えの粒度も荒くなる（ある程度データ数がないと、答えの粒度を上げることができない）

まとめ③ 分類アルゴリズムの特徴

線形分類 / SVM分類器

• データの相関が低く分散している場合に向いている
• 教師データ数が少なくてもワークしやすい
• 収束しているデータの分類に弱い、過学習に弱い
• 説明変数の尺度を適正化するデータ前処理に大きな影響を受けやすい

決定木 / ランダムフォレスト

• データが分散していてもしていなくても万能に使える
• 精度を上げるにはデータ数が必要、過学習に強い
• 前処理をあまりしなくてもワークしやすい
• ハイパーパラメータに影響を受けやすい（ノード、リーフの設定数や成立数など）

中島さん：「SVMや線形分類は、予めこういうふうに分類できたらいいなという意図のもと、データをクリーニングしていけば、恣意的にワークさせることができます。そういう点では、一番コントロールしやすい機械学習モデルです」

講義を終えて

頭を使えば、お腹が空きます。仕事終わりにそのままTTTに参加した方は、夜の22時をまわり空腹マックス……。

ビールやお茶を手にみんなで乾杯！ピザをほお張りながら、中島さんと参加者たちは親睦を深めました。

今回TTTのテーマを聞いたとき、非エンジニアの私が果たして理解できるのか、そして記事を無事執筆できるのかとても不安でした。

受講を終えて、難しい部分は確かにありましたが、それぞれの機械学習アルゴリズムの基本的な特徴や使い勝手をやさしく解説していただいたので、基本的なポイントは掴むことができたように感じています。

GIGは定期的に社外のスペシャリストをお招きして、勉強会を開催しています。イベントの詳しい情報は、GIGのconnpassページで発信中。気になる回があれば、お気軽にご参加ください！GIG社員一同お待ちしております。

GIG BLOG編集部

株式会社GIGのメンバーによって構成される編集部。GIG社員のインタビューや、GIGで行われたイベントのレポート、その他GIGにかかわるさまざまな情報をお届けします。